| Lazy Reaction |
| INTENTION |
This pattern is applicable if the truth value of phenomenon, represented by
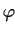 (usually instantiated by a predicate symbol), is defined in
dependence on another phenomenon, represented by
(usually instantiated by a predicate symbol), is defined in
dependence on another phenomenon, represented by 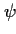 .
The kind of
dependence considered here means, that the phenomenon represented by .
The kind of
dependence considered here means, that the phenomenon represented by 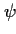 has to be true for a specific time span in the past.
has to be true for a specific time span in the past. |
| SIGNATURE |
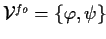 , ,
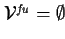 , ,
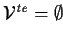 , ,
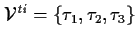 |
| FORMAL |
![$\square( \varphi \leftrightarrow (\blacksquare_{\le \tau_1} \psi) \vee
(\langl...
..._2} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) )$](img7.gif) |
| NATURAL LANGUAGE |
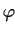 always holds if and only if one of the following conditions
holds:
always holds if and only if one of the following conditions
holds:
- during the past
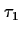 time units
time units 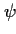 has continuously been
true
has continuously been
true
- there has already been a time span of length
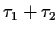 time
units such that
time
units such that 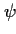 has continuously been true, and since this
has been the case for the last time, periods where
has continuously been true, and since this
has been the case for the last time, periods where 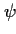 was false
continously were not longer than or equal to
was false
continously were not longer than or equal to 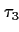 . .
|
| Examples |
| EXAMPLE 1 |
| |
FORMAL |
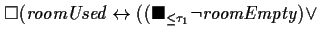
![$(\langle * [ \blacksquare_{\tau_1 + \tau_2} \neg
\mathit{roomEmpty} ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \neg \mathit{roomEmpty})
))$](img13.gif) |
| |
NATURAL
LANGUAGE |
A room is currently in use (represented by
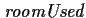 if and only
if one of the following conditions holds:
if and only
if one of the following conditions holds:
- during the past
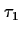 time units a room has continously been not
empty;
time units a room has continously been not
empty;
- there has already been a time span of length
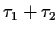 time
units such that a room has continuously been not empty, and since
this has been the case for the last time, periods where the room was
empty continously were not longer than or equal to
time
units such that a room has continuously been not empty, and since
this has been the case for the last time, periods where the room was
empty continously were not longer than or equal to 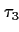 . .
|
| Theorem Part |
| THEOREM SIGNATURE |
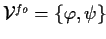 , ,
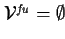 , ,
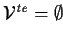 , ,
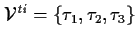 |
| THEOREM 1 Simplification 1 |
| |
FORMAL |
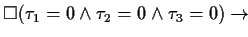
![$(\square( \varphi \leftrightarrow (\blacksquare_{\le \tau_1} \psi) \vee
(\lang...
...} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) ) )$](img16.gif)
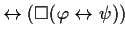 |
| |
EXPLANATION |
This theorem expresses in which way this pattern can be simplified if all
time designators are 0. |
| THEOREM 2 Simplification 2 |
| |
FORMAL |
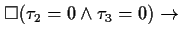
![$(\square( \varphi \leftrightarrow (\blacksquare_{\le \tau_1} \psi) \vee
(\lang...
...} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) ) )$](img16.gif)
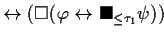 |
| |
EXPLANATION |
This theorem expresses in which way this pattern can be simplified if the
time designators 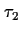 and
and 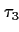 are 0.
are 0. |
| THEOREM 3 Simplification 3 |
| |
FORMAL |
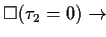
![$(\square( \varphi \leftrightarrow (\blacksquare_{\le \tau_1} \psi) \vee
(\lang...
...} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) ) )$](img16.gif)
![$\leftrightarrow(\square( \varphi \leftrightarrow (\langle * [
\blacksquare_{\l...
...1} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) ))$](img22.gif) |
| |
EXPLANATION |
This theorem expresses in which way this pattern can be simplified if the
time designator 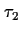 is 0.
is 0. |
| THEOREM 4 Simplification 4 |
| |
FORMAL |
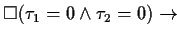
![$(\square( \varphi \leftrightarrow (\blacksquare_{\le \tau_1} \psi) \vee
(\lang...
...} \psi ] \Rightarrow \rangle
\blacksquare\blacklozenge_{\le \tau_3} \psi) ) )$](img16.gif)
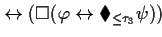 |
| |
EXPLANATION |
This theorem expresses in which way this pattern can be simplified if the
time designators 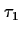 and
and 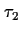 are 0.
are 0. |
![[logo of the networked systems group]](/en/images/vs.gif)
